Погружение в глубокое обучение: Как учить и не учить математике
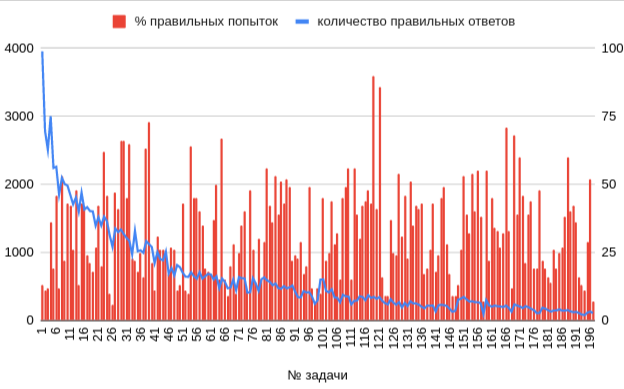
Количество успешных решений и процент успешных попыток отправки решений задач в курсе.
Мои заметки о погружении в глубокое обучение:
Чёрт дёрнул вспоминать вышку. Я планирую немного забатанить машинное обучение, но сперва решил вспомнить, чему меня в университетах учили. Тем более, что математического анализа мне иногда не хватает.
Поэтому я нагуглил на Stepik курс с пятью звёздами сразу в двух частях (1, 2) за авторством Александра Храброва.
Первую часть я прошёл за 6 полных дней на 100%. Вторую, с перерывами, дней за 10 на 87%: стало жалко времени и сил. График в заголовке намекает на причину :-)
Попутно накопил заметок о курсе, о том как «правильно» учить математике. И как ей учить не надо.
Само собой, всё с моей колокольни.
Позитивное
В целом, курс имеет право на существование.
Автор хорошо объясняет те части, которые объясняет. Половина заданий выглядит подходящими для проверки знаний и набивания руки.
Если вы ориентируетесь в математике или, что лучше, до этого учили вышку , то курс поможет вспомнить забытое. Вот я в школе в математических олимпиадах участвовал, в вузе на 9-10 вышку сдавал и через некоторую боль курс осилил :-D
Если вы учитесь в Академическом университете, то курс тоже вам подойдёт, потому что это запись лекций из него.
В противном случае вас ждут…
Боль и страдания
Видели график в заголовке? Я не поленился и для всех задач курса выписал количество успешных решений и процент успешных попыток отправки решений. Уже на середине первой части я твёрдо решил этот график нарисовать.
Из начинавших курс 4000 человек до конца дошло около 100. Конверсия 2.5%!
Безотносительно качества и рейтинга у меня есть большие сомнения в целесообразности траты сил на оформление курса, который проходит 2.5% учащихся. Какое мнение о математике сформируется у остальных 97.5%?
У меня есть профессиональная деформация — когда я что-то делаю, пытаюсь помещать себя в шкуру других людей. Например, людей, которые сталкиваются с математическим анализом в первый раз. Когда проходил этот курс, чуть ли не физически ощущал их боль.
Рисование совы

Первая часть курса во многом походит на известный анекдот. Вас будут учить рисовать сову.
Если у вас выработана математическая чуйка, или есть знания об общематематических приёмах, то вам будет не очень сложно перейти от кружочков к сове. Но я не представляю как это сделает человек, без математической подготовки.
Конкретные приёмы (например, выражение функции через рекуррентную формулу) и конкретная математическая область (мат. анализ) — разные вещи. Нет гарантии, что изучающий математический анализ человек владеет необходимыми приёмами общего назначения.
Если решение задачи требует нетривиального математического подхода, потрудитесь объяснить его учащимся перед задачей.
Автор же часто не даёт всей необходимой информации. Даже списка тем для самостоятельного изучения нет.
Есть рекомендации одной или двух книг. Но как искать в книге знания для решения конкретной задачи, кроме как полным прочтением книги? Если так подходить к вопросу, то зачем курс? Так-то и учебник по мат. анализу прочитать можно.
Более того, некоторые задачи даются раньше, чем объясняется как их решать. Конечно, можно догадаться, если есть опыт и чуйка.
Магические доказательства
Когда учился в школе, университете обращал мало внимания на то, как много в преподавании математики завязано на чуйку. Огромное количество доказательств и решений производится через разного рода контрпримеры или «очевидные»/«замечательные» частные случаи.
Для «рабочих задач» использование этих подходов — хорошая практика, которая позволяет сократить объём доказательства.
Но для обучения эти подходы не пригодны. Цель учащегося — выучить некоторую математическую область, понять, что в ней как и почему. Контрпример или частный случай не дают этих знаний. Важны не они, а путь, которым математик к ним приходит. О таком пути и следует рассказывать. Его понимание и ведёт к пониманию математики.
Использование же «очевидных» решений в обучении только демотивирует учащихся, по принципу: «сам виноват, что не додумался до такой простой штуки».
Александр же контрпримерами объясняет даже решение некоторых задач. Само собой, понимание пути поиска решения такие объяснения не дают.
Ручка + бумага vs ЭВМ
Я далёк от областей с активным применением математики, но у меня есть стойкое ощущение, что в практических задачах уже давно никто не пользуется ручкой и бумагой — существует специализированный софт.
В то же время все задачи курса рассчитаны на решение дедовскими инструментами.
От трети до половины моих ошибок в задачах были вызваны потерями минусов и прочими описками.
Но ведь я пришёл учиться мат. анализу, а не переписыванию текстов. Тексты переписывали монахи в средневековье, а у нас есть Matlab, Wolfram, SymPy, Sage и прочий софт.
В итоге я поставил себе Jupyter + SymPy и дело пошло быстрее. К сожалению, SymPy не умеет всего, чего хотелось бы. Или мне надо пройти отдельный курс по нему.
В целом, я считаю, что в наше время преподавать математику в отрыве от соответствующего софта — моветон.
Ограничения Stepik
Сама платформа тоже имеет недостатки.
Главная проблема — отсутствие подсказок к решению задач. Есть только завуалированные подсказки в комментариях от других учащихся, но они не везде есть и не всегда по делу.
Сдаться и посмотреть решение тоже нельзя.
Система не принимает некоторые правильные формулы в качестве ответа к задачам. Например, E^(a*ln(x)) будет неверным ответом, а x^a — верным.
Прочие недостатки курса
Плохо объяснено что такое dx, что с этой штукой можно и нельзя делать.
Часть объяснений идёт после задач.
Условия заданий местами неполные в контексте ученика. Для преподавателя, в его контексте, задача понятна, но ученик на то и учится, что он не видит этот контекст.
Автор курса считает, что не обязательно стремиться пройти курс на 100%, но не даёт других критериев освоения курса: не маркирует задачи как опциональные, не отмечает важные/неважные темы.
Практику курс не заменит. Если вам по работе надо делать мат. анализ, то придется ещё долго набивать руку на задачах.
Как я уже говорил, и как видно из графика освоения курса, изложение сжатое, фрагментарное. Не хватает пояснений и разжёвываний.
Автор объясняет хорошо, но только то, что объясняет. А что он не объясняет — то он не объясняет :-)
Этот пост является частью серии
- Следующий пост: MIT 6.S191